Leibniz, the I Ching and the Omnibombulator

Breakthrough, influence, waiting,
splitting apart? See the solution!
The Omnibombulator is the name of a fairly well-known logic
problem, first appearing in a national newspaper back in the
1930s. The puzzle can be solved with a little deduction and
perhaps some trial and error - but there is another way, one which has striking
connections to mathematician Gottfried Leibniz's original concept of binary arithmetic and his belief in its connection with
the I Ching.
Leibniz's
claims are now dismissed but I think it is still
possible to see a strange pre-echo of binary arithmetic, modular
arithmetic and octal numbers in the old Chinese oracle - and in the
Omnibombulator. The method of divination using yarrow stalks is clearly a modulo process (repetitive division noting the remainders, the first way most of us learn to convert decimal to binary) and it is rather puzzling to me how such a method could have developed were it not for some understanding of the mathematical processes behind it. Anyway, all these coincidences of binary numbers, trigrams and octal numbers are surely too nice to ignore and the Omnibombulator (upon analysis) seems a close, if comical, cousin to the arithmometer, the first commercially produced calculator. Here is the problem followed by my guess at what would have been Leibniz's method of solution.
The Omnibombulator
This unusual instrument is operated by selecting one of the
four switch-positions A, B, C, D and turning the power on. The
effects are:
Position A - The pratching valve glows and the queech obulates
Position B - The queech obulates and the urfer curls up, but
the rumption does not get hot
Position C - The sneeveling rod turns clockwise, the pratching
valve glows and the queech fails to obulate
Position D - The troglodyser gives off hydrogen but the urfer
does not curl up
Whenever the pratching valve glows the rumption gets hot.
Unless the sneeveling rod turns clockwise, the queech cannot
obulate, but if the sneeveling rod is turning clockwise the
troglodyser will not emit hydrogen. If the urfer does not curl
up you may be sure that the rumption is not getting hot.
In order to get milk chocolate from the machine you must
ensure (a) that the sneeveling rod is turning clockwise AND
(b) that, if the troglodyser is emitting hydrogen then the
pratching valve is glowing, but that if the troglodyser is not
emitting hydrogen, the queech is not obulating. Which switch
position would you select?
If, tiring of chocolate, you wish to receive the Third
Programme you must take care (a) that the rumption does not
get hot AND (b) either the urfer doesn't curl and the queech
doesn't obulate OR that the pratching valve glows and the
troglodyser fails to emit hydrogen. Which switch position
would you select?
| P | R | U | Q | S | T | |
|---|---|---|---|---|---|---|
| A | 1 | 1 |
Continuing in this way for the other positions you get:
| P | R | U | Q | S | T | |
|---|---|---|---|---|---|---|
| A | 1 | 1 | ||||
| B | 0 | 1 | 1 | |||
| C | 1 | 0 | 1 | |||
| D | 0 | 1 |
The next part of the question gives some rules. Let's deal with the first one: 'Whenever the pratching valve glows the rumption gets hot'. For short we can put:
Rule 1: P⇒R
We are then told that 'Unless the sneeveling rod turns clockwise, the queech cannot obulate' which we can write as:
Rule 2: Q⇒S
..meaning that if the queech is obulating, then the sneeveling rod must be turning clockwise. Looking at the other information, we can get another two rules, and express them similarly. I'll use '~' to mean that something is NOT happening, so in the next rule '~T' means that the troglodyser is not emitting hydrogen.
Rule 3: S⇒~T
Finally, 'If the urfer does not curl up you may be sure that the rumption is not getting hot.'
Rule 4: ~U⇒~R
..but I can write that the other way around: if the rumption is getting hot, then the urfer is curling.
Rule 4: R⇒U
I can reduce the four rules to just two. Taking Rules 1 & 4 together, I can write:
Rule A: P⇒R⇒U (now you see why I swapped Rule 4 around)
..and from Rules 2 & 3:
Rule B: Q⇒S⇒~T
Now take a deep breath. The rows of the table look like binary numbers with some digits missing - and we can treat them as such. We can look at the first three places in the grid as a three-digit binary number (call it PRU) and the second three (QST) as another. A three-digit binary number can represent any number from 0 to 7 (one octal digit) but Rule A means that for PRU some values are not allowed. It says that if the first bit is set (is 1) then so are all the others, and if the second bit is set, so is the third. In the table below only the values highlighted in green are possible. For PRU it is clear at once that of the permissible values, only 111 can fit positions A and C, only 001 can fit position B, and only 000 can fit position D. For QST, Rule B says that if the first bit is set so is the second, but the third is reset (0). Of the remaining possibilities only 110 can fit position A and B, only 010 can fit position C and only 001 can fit position D.
| PRU | QST | |
|---|---|---|
| 7 | 111 | 111 |
| 6 | 110 | 110 |
| 5 | 101 | 101 |
| 4 | 100 | 100 |
| 3 | 011 | 011 |
| 2 | 010 | 010 |
| 1 | 001 | 001 |
| 0 | 000 | 000 |
Here's the completed grid.
| P | R | U | Q | S | T | |
|---|---|---|---|---|---|---|
| A | 1 | 1 | 1 | 1 | 1 | 0 |
| B | 0 | 0 | 1 | 1 | 1 | 0 |
| C | 1 | 1 | 1 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 0 | 0 | 1 |
For hot chocolate we need {S=1, T=1, P=1} or {S=1,Q=0, T=0}. We can't get the first, but the second is in Position C, so that's the answer. For the Third Programme we need {R=0, U=0, Q=0} or {R=0, P=1, T=0}. This time the second can't be found, but the first occurs in position D. The solutions are highlighted in the grid above.
Each position of the Omnibombulator is represented by two 3-digit binary numbers, or two octal digits, just as each hexagram of the I Ching is two trigrams. Converting the binary to decimal we get 62,14,58 and 1 as the numbers of these hexagrams. It would be wonderful if these decimal representations of the binary were the traditional numbers of the corresponding hexagrams but sadly they are not - the I Ching has them as 43, 31, 5 and 23. Here are positions A to D with their binary, octal and decimal hexagrams and associated number and meaning in the I Ching:
| Hexagram | Octal | Decimal | I Ching | Meaning | |
|---|---|---|---|---|---|
| A | 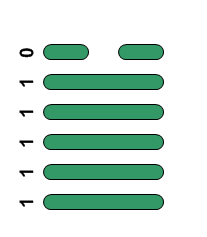 |
76 | 62 | 43 | Breakthrough |
| B | 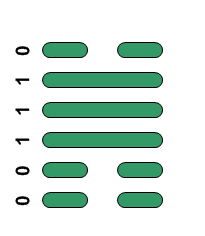 |
16 | 14 | 31 | Influence |
| C | 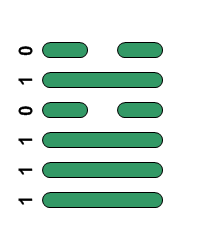 |
72 | 58 | 5 | Waiting |
| D | 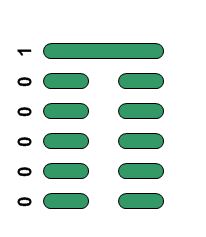 |
01 | 01 | 23 | Splitting apart |
So was Leibniz right when he suggested that in the I Ching we are looking at the work of early mathematicians, their results overlaid by later layers of ritual and superstition until understanding was lost? I think his case is not so easily dismissed. Now, I think I'll have a hot chocolate.
